"I giovani a dimostrare teoremi, i vecchi a scrivere libri!" (G. Hardy)

Bookshelf

La pagina dedicata agli scritti dei nostri lettori

Possiamo ancora fare a meno di usare la codifica Dewey, probabilmente... l'ultimo articolo caricato è il primo della lista, buon divertimento!

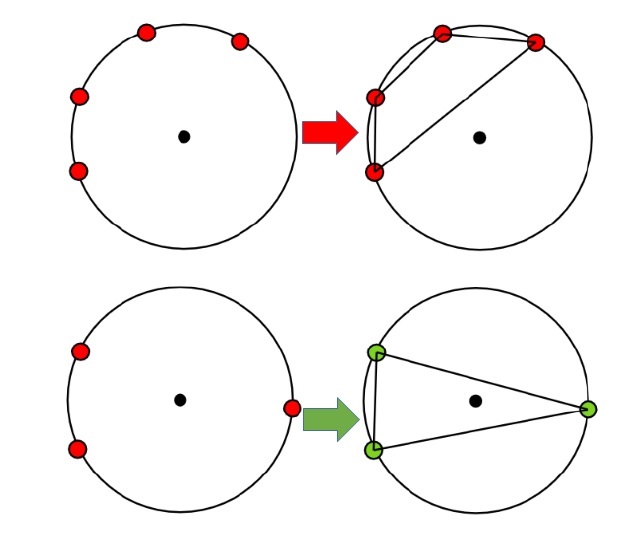Approccio ricorsivo al problema degli n punti su un cerchio [RMBSH-059]

Prendete un cerchio, e disegnate dei punti sulla sua circonferenza. Anzi no: prendete una sfera, e disegnate dei punti sulla sua superficie. Anzi no: prendete una n-sfera di dimensione 4, 5, o quella che preferite, e… troppo complicato? Allora torniamo indietro, riprendiamo il caro vecchio cerchio, la sua circonferenza, e i pochi punti che vi avevamo disegnato poco fa; li uniamo come fossero dei vertici di un poligono, e chiediamoci se il centro del cerchio finisce dentro o fuori dal poligono. Troppo facile, problema già noto e risolto? Va bene, va bene, ma se trovassimo un metodo nuovo per risolverlo, basato sulla ricorsività? Non sarebbe bello e divertente? E non potrebbe addirittura essere utile per indagare le dimensioni superiori, quelle per cui quel problema non è ancora risolto? Certo che lo sarebbe, pensa Michele Botta; per questo ha scritto Approccio ricorsivo al problema degli n punti su un cerchio. Si legge in fretta, e potrebbe stupire.

La geometria prende tutta un´altra piega [RMBSH-058]

Origami: è sempre stata una passione della Redazione di RM, e soprattutto del GC, Rudy. Così, ha iniziato a scrivere prima dei PM (Paraphernalia Mathematica) sulla nostra e-zine, poi li ha messi tutti insieme. Sono diventati così una specie di libriccino, che poi è diventato un laboratorio al Congresso UMI-CIIM di Cagliari nel 2018, ("La Geometria prende tutta una altra piega") e non è detto che che non diventino ancora qualcosa di altro nel prossimo futuro. Nel frattempo, potete scaricare il volumetto direttamente da qui...

Operatori Funzionali Vettoriali [RMBSH-057]

La matematica è uno strumento? La risposta ha quasi inevitabilmente la risposta "sì" da parte di fisici, ingegneri, ricercatori che ne fanno un uso frequente e applicativo. La risposta è probabilmente "No, o per lo meno non solo", da parte dei matematici. resta il fatto che alcune entità matematiche hanno una tale precisa funzionalità applicativa da prendere un nome che la ricorda. Il calcolo vettoriale è uno dei regali più grandi che la matematica ha fatto alla fisica, e nei nomi degli operatori si legge ancora questa eredità: un rotore non può non richiamare la fisicità di qualcosa che gira, un gradiente ricorda latinamente un gradus, un passo, una misura di avanzamento. Ma certo la sola etimologia non può bastare, e per questo è assai benevenuto questo breve saggio di Alberto Sacchi, che getta luce e ripasso su aspetti che forse non erano mai stati compresi fino in fondo.

Potenziare Pi Greco [RMBSH-056]

Sappiamo ormai da tempo che esistono infiniti numeri irrazionali, e che tra questi sono infinitamente densi i numeri trascendenti; ma, ciò non di meno, in questa infinità di trascendenti brillerà sempre di luce maggiore, ferma e decisa, il trascendente per eccellenza, il rapporto tra circonferenza e diametro. Non resiste al suo fascino neppure Franco Meneghin, anzi! Ci regala questo suo lavoro pregevole, il cui titolo completo è "Ricerca di una serie convergente a π e suo binomio di potenziamento", e bisogna riconoscere che è tutto un programma. Franco ci si è dedicato anima e corpo per molto tempo, merita certo di essere letto.

Amiche delle Stelle [RMBSH-055]

Quel che piace a Luisa Spairani è raccontare storie sulle donne. Ne abbiamo già avuto ampia dimostrazione con il racconto di Grace Murray Hopper. Quel che piace a Luisa Spairani è raccontare storie di Astronomia. Ne abbiamo già avuto ampia dimostrazione cone il suo pezzo sugli Herschel. Poi, le piace anche il teatro. Ebbene: donne, astronomia e teatro sono tutti insiemi qui, in questo pezzo!

Concetti e Attributi [RMBSH-054]

Uno dei maggiori contribuenti di questo Bookshelf di RM, è ormai evidente, è il nostro Guido Fiorentino. Per quanto abbia contribuito con testi su argomenti diversi, è ormai palese che il suo interesse cruciale è quello relativo alla distinzione tra "concetti" e "attributi" nella logica classica e moderna. Con questo scritto torna sul suo argomento preferito.

Sui problemi di Hilbert [RMBSH-044]

Guido Fiorentino , coerente con i suoi scritti precedenti, continua ad analizzare le distonie della matematica moderna che a suo giudizio discendono da un peccato originale, la mancata distinzione cruciale, negli oggetti matematici, tra "concetti" e "attributi". In questo scritto analizza, in quest´ottica, i principi fondamentali che stanno alla base dei famosi 23 problemi che David Hilbert propose alla comunità dei matematici al Congresso di Parigi del 1900.

Ricorsione e gettoni di due colori [RMBSH-043]

Carlo il Grande è uno dei più continui e precisi solutori dei nostri problemi proposti su Le Scienze, dove ricompaiono anche spesso i nostri articoli già passati sulla rivista. Tra i commenti Gnugnu proponeva un quesito supplementare sui Mazzi di carte ben mescolati: "qual è la probabilità che ogni carta di un colore sia vicina ad almeno una dell’altro?”.
Carlo si è lanciato in una soluzione e - stimolato da Gnugnu - ha continuato ad estendere il problema, mandadoci inl risultato in due parti, la prima parte si trova seguendo il link sopra, qui la seconda parte.

L'erba dell'Ammiraglia [RMBSH-042]

Avete mai fatto il debug di un programma? Probabilmente sì. Avete mai sentito parlare di Grace Murray Hopper? Probabilmente no. La cosa è curiosa, perché le due azioni sono tra loro strettamente correlate. Ma siccome il personaggio di Grace merita più attenzione di un aneddoto, siamo grati a Luisa Spairani per averci mandato un altro dei suoi pezzi teatrali, attraverso il quale sarà possibile conoscere - e immaginare - qualcosa di più su questa grande donna, ancora troppo poco nota anche tra gli addetti ai lavori. .

Tra il Cielo e la Terra [RMBSH-041]

Noi ci vantiamo spesso di essere stati tra i primi (perlomeno in Rete, perlomeno in Italia) ad aver approcciato la matematica e la scienza in maniera insolita, diciamo "colloquiale", anche se il termine più giusto potrebbe essere "caciarona". Lo abbiamo fatto perché la cosa ci divertiva, ma sappiamo benissimo che della scienza si può parlare in molti modi attraenti, meno ingenui dei nostri, ma non certo meno piacevoli e ricchi di emozioni. Ad esempio, Luisa Spairani preferisce scrivere di scienza con narrazioni che sembrano fatte apposta per essere messe in scena, e ci piacerebbe davvero vederne il risultato in un teatro. Questa breve "piece", ad esempio, alza il sipario su uno dei grandi dell'astronomia, John Herschel.

Concetti e Attributi [RMBSH-040]

Lo abbiamo detto molte volte, e ci aspettiamo di doverlo ripetere ancora spesso: più ancora delle capacità logiche, razionali, deduttive, è la passione per gli argomenti che rendono un uomo capace di dedicare tutto sé stesso alla ricerca della conoscenza. Questo è ormai del tutto evidente nel caso di Guido Fiorentino , che torna ad analizzare con tutta la sua profondità quali siano i rischi della logica predicativa, e la necessità (in fondo non dissimile da quella che sentiva prepotente anche Peano, nei suoi ultimi anni di vita) di giungere ad una definizione univoca e inattaccabile dei concetti e dei predicati. Guido è tornato, dopo la prima versione del 2012, a riproporre meglio la sua analisi del linguaggio e della logica

Fermat e Tartaglia: alcune condizioni di primalità [RMBSH-039]

In questo elenco di articoli del Bookshelf non dovreste avere difficoltà a trovare, appena qualche casella più sotto, il precedente lavoro di Antonio Rita, intitolato "I Quadrati di Galileo". In questo suo secondo pezzo Antonio ritorna e sviluppa il suo argomento preferito, e sembra proprio che abbia intenzione di concludere con un terzo articolo questa sua trilogia. Trilogia che si capisce abbastanza bene, se avrete intenzione di leggerlo, dove è destinata ad atterrare. Ma per arrivare al tre bisogna passare dal due, come insegnano i maestri alle elementari, quindi è opportuno procedere per gradi.

Un esperimento mentale sui fondamenti della logica matematica [RMBSH-038]

Di esperimenti mentali è piena la storia della scienza, specialmente di quella disciplina scientifica che degli esperimenti (reali) fa il suo pane quotidiano. La logica, e in particolare la logica dei fondamenti della matematica invece è solitamente ricca di argomentazioni "mentali", ma non troppo abituata al concetto di "esperimento". Ciò nondimeno, il nostro Guido Fiorentino torna di nuovo all'attacco della logica fondamentale, e suggerisce di prendere in considerazione come potrebbe essere la logica qualora la distinzione tra "concetto" e "attributo" fosse davvero portata alle sue conseguenze finali. L'esperimento si può fare anche solo leggendo questo articolo, vale la pena provarci.

L'arma spuntata di Popper [RMBSH-037]

Se c'è una cosa che ormai i lettori di questo Bookshelf sanno per certo, è che il nostro Guido Fiorentino è davvero molto interessato agli aspetti filosofici - e soprattutto logici - dei fondamenti della matematica e del linguaggio scientifico. In questo suo lavoro - come al solito originale e sorprendente - mette uno contro l'altro due mostri sacri della filosofia della scienza del Novecento: Kurt Gödel e Karl Popper. L'uno armato di "incompletezza", l'altro di "falsificazione". Il risultato, inutile dirlo, è tutt'altro che scontato...

Variazioni sul Teorema di Morley [RMBSH-036]

Come è facile vedere anche solo risalendo questa ormai lunga lista di articoli, il primissimo pezzo che ha inaugurato, ormai diversi anni fa, il Bookshelf di RM è stato un articolo scritto dal nostro GC in merito al Teorema di Morley: un teorema affascinante soprattutto perché ha il pieno sapore delle dimostrazioni euclidee, pur essendo tutt'altro che antico. Il suo fascino è ancora intatto, e infatti Paolo Da Ponte ha dedicato tempo ed energie a sviluppare un tema costruttivo il cui spunto iniziale deriva proprio dal teorema di Morley, sia pure nella sua forma limite che considera due lati del triangolo "paralleli". Da qui passa allora dai triangoli ai rettangoli, e quel che ne risulta sono delle costruzioni che potete ammirare direttamente in quest'articolo.

I Miracoli della Negazione [RMBSH-035]

A scorrere i titoli - e i nomi degli autori - di questo Bookshelf di RM, si notano certo dei punti di accumulazione. Accumulazione di interesse, in questo caso: ci sono appassionati di geometria e di algebra, di probabilità e di teoria dei numeri. In questo novero, è indubbio che il nostro affezionato Guido Fiorentino sia davvero intrigato dai lucenti misteri della della Logica. Con questo suo nuovo articolo (che l'autore stesso non esista a definire "una provocazione"), Guido esplora fino a che punto si possa spingere l'uso (e l'abuso) del più naturale degli operatori logici: quel "NON" che dichiara sfacciatamente la diversità. Guido ama la logica, e quindi la dialettica: nel caso qualcuno volesse rispondere alla sua provocazione, sarà ben lieto di farlo. E noi, inutile dirlo, saremo ben lieti di pubblicare...

Un'utile proprietà? [RMBSH-034]

La cosa più curiosa è il punto interrogativo nel titolo. Ce lo ha messo già l'autore del pezzo, Arcangelo Muschitiello, e non saremo certo noi a toglierlo. Un po' come se lo stesso Arcangelo di chiedesse se la proprietà che ha ricercato possa o meno avere davvero una sua utilità: gioca infatti nell'inversione degli estremi dei numeri, e nel farlo sviluppa un testo povero di parole e ricco di formule. Se la domanda era rivolta a noi, alla Redazione di RM, non esitiamo a confessare che non lo sappiamo, e proprio per questo la sottoponiamo al vaglio dei nostri esperti, cioè i lettori di RM. Ma, per quel poco che conta, qualsiasi studio che analizza come si possa cambiare punto di vista (come nel caso degli estremi dei numeri) a noi è istintivamente simpatico.

I Quadrati di Galileo [RMBSH-033]

Pochi nomi sono noti ai fisici più di quello di Galileo. E ancor meno sono i teoremi che possono competere in fama con l'Ultimo Teorema di Fermat. Ebbene, c'è chi tra il padre della Fisica e il Mostro Sacro della Matematica ha rinvenuto dei legami e dei rapporti particolari; e, non a caso, si tratta di rapporti che affondano radici in conoscenze ancor più remote nella storia della scienza, visto che le prima vestigia di questa relazione possono farsi risalire al terzo secolo avanti Cristo. Ad indagare su questi rapporti è stato Antonio Rita, e un assaggio dei suoi studi li potete trovare in quest'articolo sui "quadrati" di Galileo.

Alla ricerca dei primi [RMBSH-032]

I frequentatori di questa poliedrica pagina del sito di RM già conoscono Marco Ripà, perchè alcuni suoi lavori sono presenti proprio nelle righe precedenti di quest'elenco. Il titolo del documento che si apre cliccando questo link è un altisonante "Strutture modulari associate al problema della primalità nelle sequenze concatenate", e ha l'indubbio vantaggio di spiegare per esteso il proprio contenuto. A noi non resta che lasciarvi la possibilità di leggerlo...

Numeri a N dimensioni [RMBSH-031]

Sono celebri i quaternioni di Hamilton, e se girate da qualche parte nel sito di RM, ne troverete diverse tracce. Ma, in fondo, il "quater" di "quaternione" sta lì a ricordare solo la quarta dimensione, e sappiamo tutti che, matematicamente parlando, quattro non è che un numero come gli altri. Se avrete la pazienza di leggervi questa lunga memoria scritta da Nicola D'Alfonso, scoprirete come sia possibile superare il banale conteggio delle dimensioni sulle dita della mano, e passare al più generico, e matematicamente attraente, "N". Un paio di avvertenze: primo, si tratta di un'opera lunga, circa 125 pagine, e non va pertanto presa alla leggera. Secondo, è possibile che la sua natura e le sue conclusioni siano degne di palcoscenici più nobili del nostro bookshelf; vi avvertiremo qualora riviste accademiche e specializzate dovessero pubblicarla; ve ne renderemo edotti, e renderemo il giusto merito all'autore. Per il momento, Nicola ci autorizza a farvela vedere, leggere, studiare. Beh, fatelo, no? Potrebbe essere una vera "anteprima"...

La Teoria dei Tratteggi [RMBSH-030]

Bisogna riconoscere che Simone Battagliero tiene ben fede al suo cognome. Non tanto per le sue caratteristiche belliche, quanto per la capacità di esplorare territori inesplorati. Nonostante la sua giovane età, Simone ha dedicato molte energie nella costruzione ab ovo di una teoria matematica che ha chiamato Teoria dei Tratteggi. Ha costruito un vasto sistema, e ci chiede di verificare se la sua costruzione è davvero originale, o utile, valida. Noi, naturalmente, abbiamo subito chiarito che di matematica non capiamo niente, ma ci siamo offerti di ospitare una sua presentazione della teoria in questa sede: il documento che si può leggere cliccando sul link è infatti solo una breve sintesi della sua opera, che occupa ormai un paio di centinaia di pagine (il link al testo completo è naturalmente presente nel documento di sintesi). Se qualche volenteroso ed esperto lettore di RM volesse dargli uno sguardo, e commentare il lavoro, Simone (e noi con lui) ne sarebbe felice.

La Matematica dei Munduruku [RMBSH-029]

Ospitiamo molto volentieri un nuovo scritto di Guido Fiorentino che è solito esplorare aspetti interessanti della logica e della filosofia. In questo suo breve lavoro Guido esamina alcune caratteristiche davvero curiose della matematica e logica implicite nel linguaggio di una tribù dell'Amazzonia, i Munduruku, appunto. La bambina che occhieggia nella foto qua a sinistra, oltre che bellissima, è proprio una Munduruku.

Immarcescibili Noci di Cocco [RMBSH-028]

Il problema dei naufraghi che - con o senza scimmia di accompagnamento - si dividono in maniera teoricamente equa ma praticamente truffaldina un mucchio di noci di cocco è veramente un classico della matematica ricreativa. Noi ne abbiamo parlato spesso, anche sul blog che teniamo per conto di "Le Scienze". Il nostro Nino Giacalone, dalla bella Palermo, dice che i concetti di "equazione diofantea" e quello di "noce negativa" lo spaventano molto, e ha provato a risolvere il classico con un approccio diverso. La nostra sensazione è che, nonostante la sua modestia, Nino sia effettivamente riuscito a risolvere la diofantea, ma - come sempre in questi casi - preferiamo che siate voi a decidere se la nostra impressione sia giusta.

Ricorsivtà d'una particolare classe di interi [RMBSH-027]

Sempre l'inquieto Marco Ripà ci propone anche qualche caratteristica ricorsiva di alcuni interi particolari (potreste guardare la figura qua a fianco per avere una mezza idea di che tipo di interi stiamo parlando). Sempre molto sintetico e veloce nell'esposizione, il contenuto della quale potrebbe incuriosire.

Una curiosa proprietà [RMBSH-026]

La curiosa proprietà è quella che ritiene di aver scoperto Marco Ripà, e ci tiene a farlo sapere alla vasta e spietata comunità dei lettori di RM. Si tratta solo di una mezza paginetta, vale la pena dargli uno sguardo: e poi fateci sapere cosa ne pensate.

1° Test di primalità di VincS [RMBSH-025]

La ricerca dei numeri primi è da sempre uno dei campi più affascinanti della matematica. Ha un fascino diretto e immediato, che colpisce sia i grandi matematici che coloro che si avvicinano solo saltuariamente alla scienza dei numeri. VincS, nella sua esplorazione dei numeri “mattoni dell’aritmetica” ritiene di aver trovato un test di primalità originale, che pubblica in questa nostra rubrica. È molto orgoglioso della sua scoperta, e a noi non resta che invitare tutti i lettori di RM a prenderne visione, verificare, e commentare.

Essere o non essere, non è questo il problema [RMBSH-024]

Abbiamo già incontrato la penna di Guido Fiorentino, che proprio in questa pagina è presente con uno scritto che non si può oggettivamente definire matematico nel senso comune del termine, ma che ha uno spessore meditativo che al pensiero matematico non è nuovo. Anche perché l’oggetto dell’indagine di Guido è pur sempre il linguaggio, e non è nuova la considerazione che la matematica sia anche, se non soprattutto, un linguaggio dalla precisione ancora ineguagliata. In questo suo lavoro dal titolo quasi amletico si ritrovano considerazioni della stessa natura, una digressione semantica e semiologica che potrebbe illuminare chi intende percorrere i sentieri di confine tra matematica, logica, filosofia e metafisica.

Dissertazioni matematiche sulla (non) esistenza di Dio [RMBSH-023]

Marco Giancola è affascinato da quegli aspetti della matematica che possono dare adito ad esplorazioni ideali e conclusioni metafisiche. Questo campo conta certo dei predecessori illustri, tutta una serie di pensatori che hanno provato, da Pascal a Kant, da Cartesio a Leibniz, da Gödel fino agli scritti più vicini a noi di Piergiorgio Odifreddi, a tirare conclusioni sull’esistenza – o non esistenza – di Dio. Tra prove ontologiche, teleologiche, antropiche o trascendentali, questo scritto racconta quale sia, in merito, la conclusione di Marco.

Tesi di Laurea Magistrale su Rudi Mathematici [RMBSH-022]

Voi non la conoscete, ha gli occhi belli..." i meno giovani staranno già completando il verso della canzone (urlando a squarciagola "Eulalia Torricelli dal Forliiiì...", ma noi in realtà ci stiamo riferendo a Francesca Gaggioli, dottoressa magistrale in Comunicaziione Multimediale e di Massa, che si è laureata il Sei Novembre 2010 con una tesi dal coraggioso titolo "Rudi, si fa per dire". L'argomento della tesi dovrebbe essere evidente, visto il titolo e visto il luogo dove leggete queste righe. Però noi ancora facciamo fatica a crederci. Da quel sei novembre non facciamo altro che andare in giro con una spettacolare coda di pavone. La tesi è ricca di figure, e quindi voluminosa. La abbiamo spezzettata, ma la trovate tutta qui, se volete. Introduzione, Capitolo 1.1 (prima parte), Capitolo 1.1 (seconda parte), Capitolo 1.2, Capitolo 2.1, Capitolo 2.2, Capitolo 3.1, Capitolo 3.2, Capitolo 4.1, Capitolo 4.2, Conclusione e bibliografia. Resta altro da dire? beh, sì... almeno un paio di parole: grazie, Francesca.

Questa storia potrebbe intitolarsi "Galassia che vai"? [RMBSH-015]

Questo, a sentire l'autore, è classificabile come romanzo itinerante. Di certo è qualcosa di insolito, che intende mescolare matematica e narrativa, e nel farlo si impone dei vincoli assai stringenti. Per capire meglio di che opera di tratta, conviene leggere le istruzioni per l'uso, che saggiamente, sono state messe all'interno del racconto stesso. Quel che possiamo anticiparvi in queste poche righe è che l'autore di cotanta opra è Martino Benzi che ha tutte le intenzioni di sviluppare la storia in parallelo agli sviluppi di RM. Una sfida a metà tra la Conquista dello Spazio e le Mille e Una Notte, che dovrebbe cominciare proprio qui. Abbiamo detto "cominiciare"? Seeeh... la storia procede e prolifica da mesi, ormai. C'è già un romanzo di quasi 200 pagine, da leggere...

Tempi (polinomiali) di esecuzione di nvariabili [RMBSH-021]

Luigi ci ha scritto, dicendoci: "Qualche volta, stanco di leggere, mi metto a scrivere. Ed è così che ho partorito una "presunta" dimostrazione che il problema 3Sat è risolvibile in tempo polinomiale. Ha richiesto tempo e fatica: pensavo che il grosso fosse fatto, ma ecco che mi scontro con un ostacolo quasi insormontabile: nessuno mi dice né sì né no. Eppure a me basterebbe poco: 1) Una persona con la mente aperta che leggesse ciò che ho scritto 2) Mi segnalasse il più catastrofico degli errori commessi 3) Ne concludesse che sono un imbecille". Noi in matematica non siamo tanto forti, ma da quel che abbiamo letto ci sentiamo di escludere che Luigi sia un imbecille. Visto che abbiamo già eliminato il punto 3), c'è qualcuno che ha voglia di cimentarsi con gli altri due? A noi sembra che il lavoro di Luigi Salemi, possa interessare chi è affascinato da tutta la problematica P vs NP.

Divisibilità per 3 degli elementi di alcune sequenze numeriche [RMBSH-020]

Dice il nostro eroe: "L'articolo consta di 3 parti distinte, ma fortemente correlate e sequenziali: nella prima viene dimostrato che i soli possibili termini-primi della "sequenza consecutiva" (1,12,123,1234...) sono solo il 13.3% del totale e viene esplicitata la forma che hanno. Il risultato viene allargato a tutte le permutazioni delle cifre degli stessi. Nella seconda sezione applico quanto appena visto ad un sottogruppo consistente di elementi della sequenza circolare (derivante da quella consecutiva), individuando altresì suoi primi 25 termini-primi. Viene fornito dunque un criterio (ulteriormente estendibile) che riduce progressivamente la numerosità dei "candidati numeri primi". Nell'appendice 2 viene invece risolto un problema affine, risalente al 1996. Infine, nell'ultima parte, introduco una nuova sequenza, caratterizzata dalle stesse proprietà delle precedenti, ma molto più "vasta"; proponendo anche alcuni quesiti aperti." A cotanta presentazione scritta direttamente da Marco Ripà, possiamo forse aggiungere qualcosa? Certo no. Voi però sì, potete: e potete mettervi a leggere, tanto per cominciare.

La Corona di Archimede [RMBSH-019]

Come Archimede riuscì a smascherare la truffa ai danni di re Gerone di Siracusa è storia più che nota, addirittura celeberrima. La composizione della corona d'oro, narra Vitruvio, fu rivelata da Archimede grazie alla sua recente scoperta della spinta idrostatica, da allora chiamata appunto "archimedea". Come sempre accade, gli aneddoti tendono un po' a semplificare i concetti: un po' per fini narrativi, un po' per fini esplicitamente didascalici. Di certo, non appena si prova ad analizzare un po' meglio i dettagli della narrazione, si scoprono cose decisamente più complicate, e per questo interessanti. E' quello che ha fatto il nostro Felice Costanti, e il risultato è stato così interessante da meritrsi la pubblicazione su un prestigioso volume della Springer. Volume che però è davvero costoso, e non possiamo permettercene neppure una copia per recensirlo per intero. Speriamo che la Springer stessa non si arrabbi se mettiamo a disposizione l'articolo di Felice qui. Nel caso si arrabbiasse, sia ben chiaro che la colpa è nostra, non di Felice.

Logica e Linguaggio [RMBSH-018]

Frege sosteneva che la matematica discendesse interamente dalla logica: si sbagliava, come gli mostrò spietatamente Russell. Pur senza essere l'unico, la logica resta ugualmente un elemento fondante della matematica. E, a sentire molti, la matematica è anche e soprattutto un linguaggio. Forse è per questo che Guido Fiorentino ha deciso di scrivere un articolo che tende ad esplorare entrambi gli aspetti. Per far parlare direttamente l'autore: l'articolo cerca di dare una risposta alla complessa domanda: "L’usuale logica aristotelica consente di utilizzare espressioni del tipo “~A” (o “¬A”), senza preoccuparsi del significato metamatematico di “A”, se – per citare il caso più frequente - sia un aggettivo o invece un sostantivo. Ha però un qualche reale significato il negato di un sostantivo, che assomma tutto ciò che esso non è?". Non è un articolo canonicamente formale, è lui il primo a sostenerlo: noi, comunque, incapaci di giudicarlo appieno perchè palesemente troppo poco ferrati nel campo, ve lo sottoponiamo volentieri qui.

Modello di matematica concettuale [RMBSH-017]

Dobbiamo riconoscere che quest'articolo di Matteo Pazzi è davvero insolito. Partendo letteralmente dal nulla (anzi: dal nulla e dal tutto, per omogeneità formale) Matteo prova a costruire appunto un nuovo "modello di matematica concettuale", nè algebrica nè geometrica. E la sua intenzione è quella di trovare le relazioni di base con la fisica. Se volete provare a seguire i suoi ragionamenti, potete farlo qui.

WinForLife [RMBSH-016]

Abbiamo lettori attenti e animati da ottime intenzioni. Uno dei migliori utilizzi possibili del calcolo delle probabilità, ad esempio, è senza dubbio il mostrare quanto sia difficile - e soprattutto poco conveniente - dedicarsi al gioco d'azzardo. In buona sintesi, questa è proprio la missione di Paolo Canova e Diego Rizzuto, che vanno in giro per la nazione ad illustrare le perverse tentazioni del tirare a sorte. In questa paginetta, raccontano quanto siano stati sfortunati alcuni vincitori del gioco più alla moda, il Win For Life. E il fatto che di tale "sfortunata fortuna" abbiano parlato così poco i media dovrebbbe farci riflettere. Trovate il loro articolo qui.

Legge e Ordine [RMBSH-014]

Come insegna Gadda, alcuni dei migliori scrittori sono ingegneri. Quando, in RM133, il Gran Capo ha concionato di Computer Quantistici nel suo PM, non poteva certo immaginare che stava scoperchiando un vaso di Pandora. Il grande Martino Benzi ha rispolverato un suo vecchio racconto per l'occasione (chi non ha un racconto su Computer Quantistici nel cassetto, del resto?) e ce l'ha mandato. Se siete curiosi di capire cosa c'entri la computazione quantistica con la stella di sceriffo qui a fianco, non dovete far altro che cominciare a leggere qui.

Regali di Compleanno a Rudy, Alice e Piotr [RMBSH-013]

Nel 2009, ogni elemento della Redazione ha ricevuto un regalo di compleanno da un affezionato lettore; anzi, diciamo meglio: da un Instancabile Fustigatore. Il nostro misterioso autore è certo affezionato, infatti: lo dimostra il fatto stesso che ci abbia fatto dei regali; ma non di meno fustiga, perchè i regali o sono dei problemi (ben sapendo che noi siamo bravissimi a proporli, ma pessimi nel risolverli) o sono graziosi artifici per rimbrotti.
Ad esempio, il regalo per Rudy non propone un problema ma lo risolve: spiega infatti il significato geometrico della radice quadrata, rimbrottando il GC che continua a ripetere di non capire come faccia a funzionare l'algoritmo risolutivo.
Per Alice il regalo è un gioiello, e non a caso in nostro Instancabile l'ha destinato alla fanciulla del gruppo. Usa Archimede e la Magna Grecia, li coniuga con la mitologia e la geometria della Grecia madre, e il risultato è così bello che quasi ci si scorda che dentro c'è un problema da risolvere. La parte più bella è la costruzione in Geogebra di tutto il meccanismo. Il programma Geogebra può essere facilmente trovato in rete seguendo le indicazioni nel testo del problema: scaricatelo, è gratis, è bello, è soprattutto serve per godersi il regalo di Alice.
Infine il dono per il Piotr. È un racconto-regalo, ed è anche un enigma a tappe. Per risolverlo e goderselo occorre utilizzare tutto quello che si è letto nel racconto per inserirlo nel relativo programmino in Geogebra.
Le soluzioni sono qui: ma per favore, non andate a leggerle. Le soluzioni uccidono i problemi, uccidono il divertimento. Non fate come noi, voi che potete: risolvete!

Verso l'infinito, ma con calma [RMBSH-012]

Il nostro amato Zar era RMer prima d'essere un grande blogger con il nome d'arte di Proooof. Memore delle sue origini, ha generosamente accettato di veder pubblicato su queste nostre pagine il suo libro sull'Infinito dopo averlo mostrato al mondo dalle pagine del suo blog.

Telepatia e Colpi di Fulmine [RMBSH-011]

Ha vent'anni, studia Fisica, adora l'Astronomia. Come se non bastasse questo curriculum a classificarlo subito come un pericoloso e ingombrante giovane cervello (non sappiamo se già pronto o meno alla fuga), Davide Fiacconi ha anche una dote davvero insolita: la voglia di provare a misurare seriamente, con strumenti matematici, cose che di solito non si prova a misurare. Oltre alla telepatia (che potete scaricare cliccando sull'icona) ci ha inviato anche un incomparabile analisi della probabiilità di verificarsi del Colpo di Fulmine. E poi dicono che la matematica è arida...

De Poligonorum Inscriptione [RMBSH-010]

Su RM116 compare un problema piuttosto intrigante "Keplero era uno sprecone / In qualunque dimensione", destinato a far divertire un buon numero di persone (parecchie le soluzioni e variazioni sul tema che si trovano sul RM117 e RM118). Br1 ci ha inviato cinquanta pagine fitte di disegni e spiegazioni, che stanno benissimo in uno spazio di Bookshelf come questo.

Gottinga [RMBSH-009]

Mai sentito parlare di Davide Osenda? Beh, noi no, prima del giorno in cui ci è arrivato un suo fumetto di argomento matematico: lungo, interessante e bello. Si intitola Gottinga: quasi cinquanta tavole che meriterebbero di essere pubblicate in albo su buona carta. Davide ci ha autorizzato a pubblicarne una versione in bassa risoluzione, e questo ci sembra davvero un regalo. Lo abbiamo sistemato provvisoriamente qui, nella speranza che qualche editore lo porti sugli scaffali delle librerie. Prima di noi ne aveva parlato anche il blog di Andrea Plazzi, che si è così reso benemerito e al quale va riconosciuta la primogenitura dell’ospitalità. L’opera è pubblicata in osservanza della licenza Creative Commons, al solo fine di fare conoscere l’opera di Davide.

A proposito di Aeroplanini... [RMBSH-008]

Era ancora il Secondo Millennio: Dicembre 1999, undicesimo numero di RM.
Pubblichiamo il "Problema d'un altro Rudolph", che parla di numeri (grandi) e di oggetti volanti. Affrontato, sbagliato, corretto, approssimato, risolto... per molto tempo questo è stato il "Problema di RM", pur non essendo né il più difficile né il più elegante pubblicato dalla Rivista. Certo, è quello che ha più forza maieutica: è in grado di produrre opere d'arte. Lo fece prima con Sam, e pubblicammo la soluzione in RM050 (ma la riportiamo in appendice anche qui), e si è poi ripetuta con Caronte.
Sì, ci piacerebbe davvero capire cosa rende un problema "diverso" dagli altri...

Tre Dadi Duri (o Tre Sacchetti Molli) [RMBSH-007]

Ci piacerebbe scoprire quali siano le peculiarità, i criteri, i parametri che fanno sì che un problema susciti o meno interesse nella poliedrica comunità dei lettori di RM. Questo di cui riportiamo una lunga trattazione, ad esempio, è partito quasi in sordina (su RM059), per raccogliere con il tempo contributi sempre più precisi e dettagliati, fino a sfociare nella metafisica, laddove il Caso è perennemente in lotta con il Libero Arbitrio.
Molti i contributi: GaS, Mirtillo, PuntoMauPunto sviscerano il problema, aprendo la strada ad una trattazione sistematica operata da Last Duke; infine, Caronte inventa perfino un apposito sistema grafico per ridurre definitivamente il problema alla ragione.

La Caduta della Fenice [RMBSH-006]

Chi di tesina ferisce, di tesina perisce: anche questa, come la precedente di Sam, è infatti una tesina di maturità (classica, stavolta: non scientifica). Non vorremmo che diventasse un vizio: piuttosto, se proprio dobbiamo, preferiremmo istituire ufficialmente il GPATROM (Gran Premio Annuale delle Tesine degli RMers in Odore di Maturità)... sia quel che sia, il maturando del 2004 che si merita l'inserimento nel Bookshelf è L.A. Bachevskij (Loba per gli amici) che ci lusinga con una composizione dal sapore assai RMesco, e citandoci generosamente nella Bibliografia.

L'Intelligenza Artificiale [RMBSH-005]

Per la serie "Anche i lettori di RM, come i matematici, dovrebbero essere ammazzati da piccoli". Siamo orgogliosi di presentarvi una tesina di maturità: è quella di Sam che ormai, quando scriviamo queste righe, non si ricorderà neanche più d'essere stato un liceale. Non storcete subito il naso con aria di superiorità: se l'argomento vi interessa e non siete professionisti del campo, potreste trovarlo perfetto, come iniziazione...

Il Messaggio degli Alieni [RMBSH-004]

A dire il vero, il titolo giusto dovrebbe essere "Il Messaggio agli Alieni" perché di vero messaggio ad intelligenze extraterrestri si tratta. Però, quando lo pubblicammo per la prima volta (RM029) immaginavamo la "ricezione" del messaggio, e non la sua trasmissione. Ma comunque il titolo può andare benissimo così com'è, se si ha la piccola accortezza di ricordare che gli Alieni, in questo caso, siamo noi. Da bravo alieno, JC ha decrittato l'intero messaggio.
Siete in grado di fare lo stesso ?

I Coniglipolli [RMBSH-003]

Hanno due teste e sei zampe, e soprattutto sono assai più celebri dei loro fratelli gemelli, i conigli spollati, dotati di zero teste e due zampe. E' strano, in fondo sono nati insieme... Trovate qui uno dei frammenti poetici che più ci rallegrano, scritto da Elio Pagliarani. La poesia si cimenta con l'algebra, e questo brano lo abbiamo cercato a lungo, dopo che era stato perduto di vista nei meandri di qualche antologia liceale. Per fortuna è arrivata Valeria, che lo ha ritrovato per noi.

La Matematica delle Elezioni [RMBSH-002]

Già, è vero quasi quanto un teorema matematico: a metà legislatura, non si riesce mai a trovare un elettore che ammetta di aver votato per il governo in carica. Ma se questo vi appare paradossale, allora è sicuro che molti misteri elettorali vi sono ancora sconosciuti. Come, per dirne una, il fatto che non esiste un sistema elettorale perfetto. Se avete voglia di scoprire alcuni aspetti insoliti della democrazia, scaricatevi questa che rimane una delle migliori performance di Rudy, il Gran Capo (GC) di RM. Il "paradosso dell'Alabama" non vede l'ora di saltarvi addosso.

Il Teorema di Morley [RMBSH-001]

Era l'estate del 1999, e a quei tempi bastavano due pagine per fare uno"speciale", su RM. Adesso, due pagine sarebbero considerate una "soluzione frettolosa", e tutt'altro che meritevoli di alcunché di speciale. Eppure, il Teorema di Morley è inaspettatamente bello; sembra arrivarci direttamente dalle coste spumose della Magna Grecia, ed invece è matematica recente. Recente, ma con sapore classico: dev'essere stata questa magica commistione ad indurre Rudy a scrivere questo breve pezzo per illustrarne la bellezza.